C’est une lemniscate à deux foyers, c’ est-à-dire l’ ensemble des points du plan dont le produit k²>0 de leurs distances à deux points fixes F et F’ distants de 2c>0 est constant.
Les formes ovales de Cassini diffèrent suivant que k est inférieur ou supérieur à c.
Pour k=c, c’ est une lemniscate de Bernoulli.
| Si k>c |  |
| Si k=c | 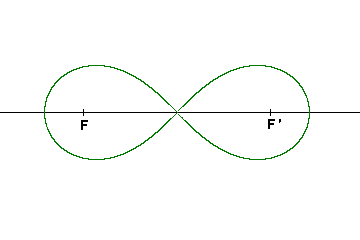 |
| Si k<c | 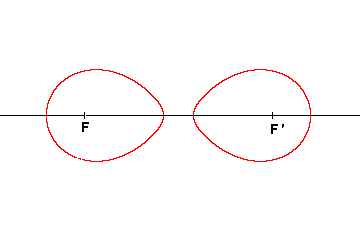 |
Lemniscate de Bernoulli
Lemniscate à deux foyers F et F ‘ dont l ‘ équation bipolaire par rapport à F et F ‘ est rr’ = k², où 2k est la distance de F à F ‘.
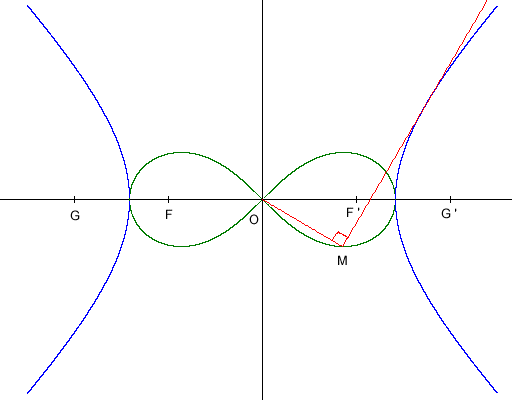
La podaire d ‘ une hyperbole équilatère de sommets A et A ‘ par rapport à son centre O est une lemniscate de Bernoulli tangente à l ‘ hyperbole en A et A ‘ et dont les foyers F et F ‘ sont les inverses des foyers G et G ‘ de l ‘ hyperbole Définition : La podaire d’ une courbe plane C par rapport à un point fixe O est le lieu des projections de O sur les tangentes à la courbe C
Si l ‘ équation cartésienne de l ‘ hyperbole est : x² – y² = a²celle de la lemniscate est : (x²+y²) = a²(x²-y²) et son équation polaire est :
r² = a²cos(2q)